Global Sensitivity Analysis Report
Experiment: F3
Started: 2022-05-24 11:26:16
Number of parameters: 5
Showing the top 5 parameters
Random Forest mean R2 score over 3 folds: 0.7148754750676094
Print report
Function Landscape
Interactive surface plot of a slice (using a Random Forest model) with X4 on the X axis and X3 on the Y axis. All other parameters are set to the center of their range.
Morris analysis results
The elementary effects calculated by the Morris [1] algorithm. On the left the covariance plot with mu_star, the absolute of the mean elementary effect, against sigma, the standard deviation of the elementary effect. Points highlighted are the parameters with the highest mu_star and these are also shown below with the confidence of the algorithm.
Sobol analysis results
Sobol Network Plot
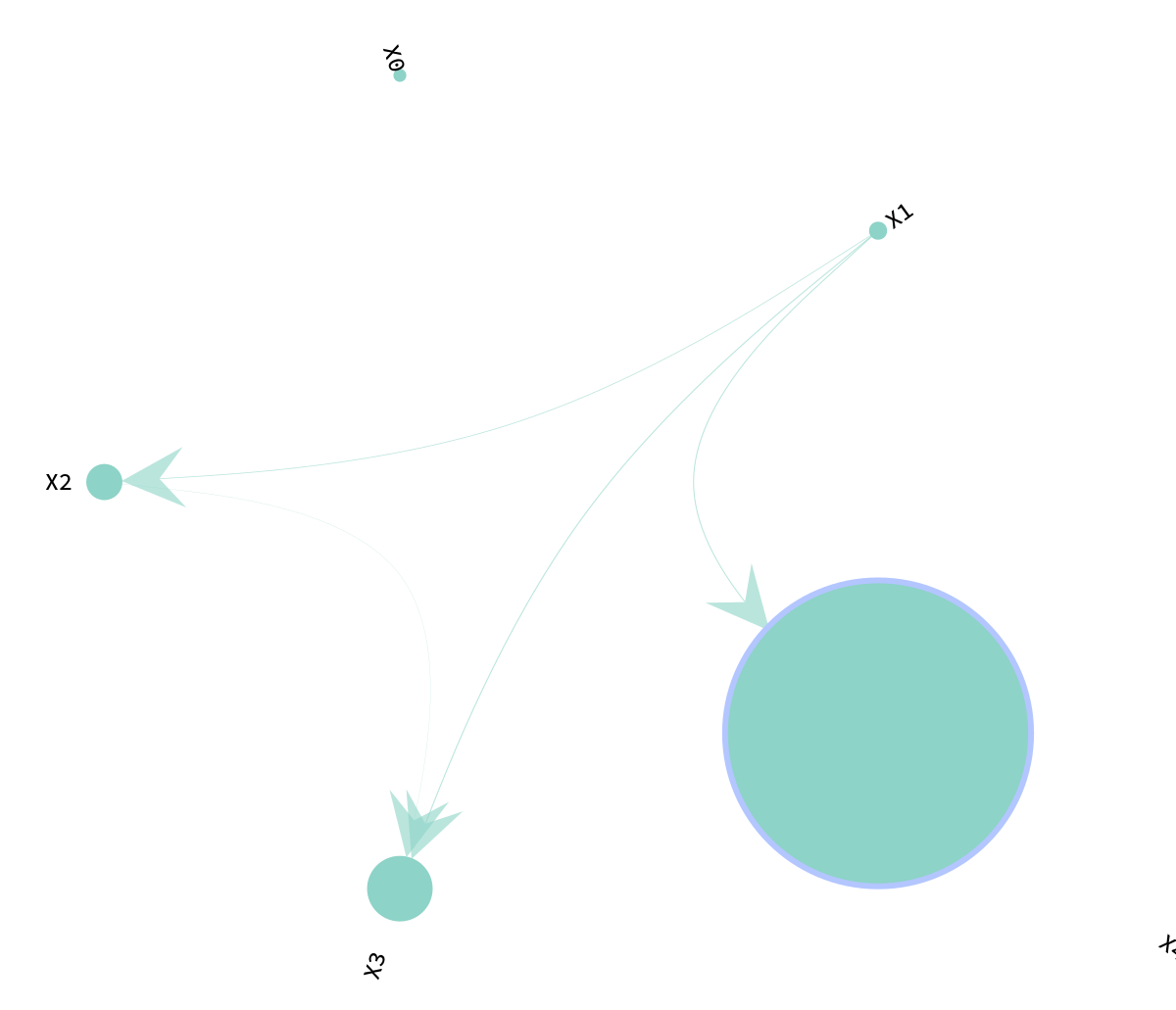
Delta
RBD Fast
Pawn
References
[1] Morris, M.D., 1991. Factorial Sampling Plans for Preliminary Computational Experiments. Technometrics 33, 161–174. https://doi.org/10.1080/00401706.1991.10484804
[2] Campolongo, F., Saltelli, A., Cariboni, J., 2011. From screening to quantitative sensitivity analysis. A unified approach. Computer Physics Communications 182, 978–988. https://doi.org/10.1016/j.cpc.2010.12.039
[3] Borgonovo, E. (2007). “A new uncertainty importance measure.” Reliability Engineering & System Safety, 92(6):771-784, doi:10.1016/j.ress.2006.04.015.
[4] S. Tarantola, D. Gatelli and T. Mara (2006) “Random Balance Designs for the Estimation of First Order Global Sensitivity Indices”, Reliability Engineering and System Safety, 91:6, 717-727 https://doi.org/10.1016/j.ress.2005.06.003
[5] Pianosi, F., Wagener, T., 2015. A simple and efficient method for global sensitivity analysis based on cumulative distribution functions. Environmental Modelling & Software 67, 1–11. https://doi.org/10.1016/j.envsoft.2015.01.004
